The Physical Properties of Data - Part 2: Working with Gunther's Universal Scalability Law
We ended The Physical Properties of Data (Part 1), with the introduction of Neil Gunther's Universal Scalability Law (USL), which states that the relationship between a system's load multiple, N, and its throughput at that load, X(N), can be described by a mathematical equation.
In this post (part 2) we will illustrate the different phases a system goes through as it scales, using analysis of the equation, alongside a more concrete example of passenger-capacity in a monorail.
Key Takeaways
The 30-second takeaway from this post, is the following:
Measure your linear scaling factor, as it defines the best-case-scenario for your system design.
Estimate or measure the critical limit value beyond which the system performance degrades if additional scaling occurs.
Make an effort to stay to the left of that point.
If your system goes over that limit, it will likely experience a cascading catastrophic failure.
This will help you understand where you are on the scaling life cycle and therefore how close or far you are at any given time to a critical failure point.
A Prelude to Math
This post includes math. You have my sincerest apology. The math is important for developing both the understanding and the intuition of what happens as systems scale, and why. In particular, the math helps us understand why and when bad things will happen, as load in our systems increases. The math is here for you to be able to calculate your own specific situation on your own, but if you're math averse or just don't feel like going through it, and just want to understand the basic concepts discussed, just skip the math and move on to the next paragraph.
The diagrams in this post illustrate the behavioural characteristics of systems as they scale, and you can develop a pretty solid intuition off of those alone.
The Math (sorry)
In his articles on the Universal Scalability Law, Gunther provides the following equation to describe the relationship between throughput and load as a system scales:
Eq. 1: The Universal Sacalability Law (USL) Equation, describing throughput, X(N) as a function of load, N.
Where:
- N is the normalized amount of input load on the system.
- X(N) is the throughput of the system at an input load N.
- 𝛾 is the constant (linear) scaling factor, which determines how quickly throughput scales as load is increased.
- 𝛼 is the contention scaling factor, which determines how quickly the throughput scaling slows down as load is increased.
- When greater than zero, this factor creates an upper ceiling, or a horizontal asymptote, which determines the absolute maximum throughput the system could ever achieve, regardless of how much load is increased.
- The value of the horizontal asymptote is
 .
.
- 𝛽 is the coherency cost scaling factor, which determines how quickly throughput decreases as load is increased.
- 𝛽 differs from 𝛼 in one key way: its association with a
 term means that at the limit of X(N), the dominant factor controlling the value of X(N) is
term means that at the limit of X(N), the dominant factor controlling the value of X(N) is  , which trends to zero. Zero throughput means catastrophic failure.
, which trends to zero. Zero throughput means catastrophic failure. - This factor determines the position of a critical load point, beyond which the system performance degrades as load is increased. Crossing that threshold will nearly always result in a cascading catastrophic failure. You always want to stay to the left of the critical point.
- The critical load point, where maximum throughput occurs is given by (when the derivative of X(n) = 0), at
 Eq. 2: The critical load value
Eq. 2: The critical load value - The maximum throughput is given by plugging Ncritical into the X(N) equation above.
- 𝛽 differs from 𝛼 in one key way: its association with a
Working with the USL Equation
It's easier to understand how these parameters work by plotting the throughput vs. load and comparing it to a relatable example.
A Monorail Loop with Two Stations
For our system, we'll use a simple monorail loop with 2 stations, A and B, and the following initial specification:
1x single-car train with a capacity of 20 passengers.
N is the number of trains on the track, starting at 1.
The train waits 1 minute at each station for passengers to get off and on.
The track is a loop so the trip from A to B rides on a different part of the track than the return trip from B to A.
The distance between the two stations is 5 miles in both directions.
Image 1: A single 20-passenger monorail, with two stations.
We can measure our train system's throughput, X, in terms of passenger-miles per hour. Including boarding time, the train takes 6 minutes to transport 20 passengers across 5 miles. 20 passengers travelling 5 miles in 6 minutes, is equal to 1,000 passenger-miles per hour.

Eq. 3: Throughput of 1 train
Simple Linear Scaling
As our city grows and ridership grows with it, we will want to increase our monorail's capacity. We can do so by adding additional trains on the track.
Gunther defines concurrency as:
CONCURRENCY or ideal parallelism (with proportionality γ), which can also be interpreted as either:
the slope associated with linear-rising scalability, i.e., the line X(N) = γ N in Fig. A when α = β = 0
the maximum throughput attainable with a single load generator, i.e., X(1) = γ
Initially, there is only 1 train, so there is no contention. As more trains are added and things are going smoothly, it's easy to mistakenly assume that the scaling factor 𝛼 is zero.
Similarly, the coherency cost factor 𝛽 is mistakenly assumed to be zero since we don't have to make allowances to mitigate contention at that stage either.
As a result, while N is still small, it appears like additional capacity scales at a constant multiple of N, the number of trains on the track.

Eq. 4: Throughput of N trains, linear
Image 2: Monorail with more trains, still operating smoothly.
Chart 1: Linear scaling, where throughput is a constant multiple of units of load in the system, shown in both linear and log-scaled load N. The remaining plots in this post will use a log scaled load N (below) to make the non-linear scaling dynamics easier to see
Chart 2: Unbounded scaling visualized as a log scaled graph
This kind of scaling is typical when the existing system's capacity is undersaturated, meaning it has not yet reached its limits. For the monorail example, this means we haven't yet reached the maximum number of trains it can support before trains have to slow down and per-passenger travel time increases.
Contention Enters the Chat
As we keep adding trains, however, reality kicks in, and our contention factor, 𝛼, begins to have an effect.
Gunther’s definition of contention is:
CONTENTION (with proportionality α) due to waiting or queueing for shared resources
We see this in the way that the growth in passenger-miles/hour slows down and eventually plateaus.
Chart 3: Bounded scaling - throughput is bounded by a horizontal asymptote at 𝛾/𝛼.
When we plot the USL with a positive 𝛼 value (dot-dashed) and compare it to the linear case where 𝛼=0 (dotted), we can see that the linear model shows a continuously increasing throughput, while in the bounded model we see that the rate at which the system throughput increases is diminishing with increasing load, and that there is an upper bound, or a ceiling, on the maximum amount of throughput the system can ever achieve.
We can rationalize this result in the monorail example, because when the trains can't clear the platform fast enough, the next train arriving has to queue up and wait. As trains queue up to wait for the trains ahead to depart the platform, the overall travel time between stations, as experienced by the passengers, increases. At the limit, the entire track is covered by trains touching front to back, and moving one platform's worth of length every minute.
Even at 10 trains, instead of each train spending 6 minutes to travel between stations, which would get us 10*1,000=10,000 passenger-mile/hour, the trains spend additional time waiting to get into the station. As a result, the trains take a little over 10.5 minutes to get from one platform to the next, with 4.5 of those minutes spent queued up, waiting to enter the station platform, or alternatively traveling at a slower speed between the stations.
Image 3: Monorail with 10 trains means that several trains now have to wait their turn to get into the two stations
That's nearly double the time of the single train with no contention, and results in a realized total throughput of 5,623 passenger-mile/hour, much lower than the 10,000 passenger-mile/hour throughput we would have liked to get!
Using 𝛾=1000 and 𝛼=0.1, we get this result from the USL equation (with 𝛽=0):

Eq. 5: Throughput of 10 trains, with contention
If you'd ever been in a traffic wave, you've experienced the exact same effect: even though there's no actual obstruction, it just takes longer to travel the same distance. Once outside of the very early linear phase of the system where the load is small, the benefit from adding additional load capacity begins to diminish.
Image 4: Phantom Traffic Jam / Traffic Wave
Source: https://www.reddit.com/r/dataisbeautiful/comments/ks6pzd/oc_numerical_simulation_of_traffic_jam_formation/
Regression Would Like a Word
As if contention alone isn't enough, as we scale our load, coherency* begins to take an increasingly expensive toll out of the throughput.
*usually it's either the cost of maintaining coherence, or the losses incurred in its absence. Either way, we lose throughput.
Gunther defines coherency as:
COHERENCY or data consistency (with proportionality β) due to the delay for data to become consistent, or cache coherent, by virtue of point-to-point exchange of data between resources that are distributed.
In other words, what we end up seeing is a performance regression caused by the increasing cost of maintaining coherency—of maintaining agreement between the different independent load processors operating in parallel. This cost comes out of the same processing capacity that is used for generating throughput, and grows with the number of independent units that need to maintain agreement.
To illustrate how this plays out in our monorail system, we'll add a secondary maintenance loop to a section of the track, which has a holding capacity of two trains.
Image 5: The main monorail loop with an additional smaller maintenance track on the left side
As the years pass and our monorail infrastructure begins to show its age, the frequency of maintenance increases. We can have two trains in the maintenance loop, but if more than 2 trains are malfunctioning at the same time, we elect to have them remain on the main track, and continue traveling, but they do not stop for passengers at the platform.
Image 6: Commuters begin to despair as several empty Not In Service trains go through the station as they wait for a working train to pick stop for them to board.
At 20 trains, we may see the following distribution of train states:
2 trains are out of commission on the maintenance track
4 trains are healthy and operational on the main track
12 trains are not-in-service but take up space on the main track and contribute to the queuing time and total travel time between stations.
We can use the 18-train throughput to compare the three models (because the 2 trains on the maintenance track don't cause additional queuing):
| Model | N | Throughput, X(N) (passenger-mile/hour) |
Travel time from A to B (including time at station B)
|
|---|---|---|---|
| Unbounded |
18 |
18,000 | 6 minutes |
| Bounded |
18 |
6,667 |
16.20 minutes |
| Bounded & Regressive |
18 |
3,125 |
34.56 minutes |
Table 1: Load, Throughput, and Travel Time for the Unbounded, Bounded, and Bounded & Regressive models, with 18 trains on the main track.
So in the bounded & regressive model, which is the model closest to reality, and which accounts for both contention and coherency effects, 18 trains on the track are barely more effective than 3 trains. In other words, 83% of the trains aren’t adding value in terms of passenger-mile/hour throughput.
But it's actually worse, because not only are we using 18 trains to achieve the passenger throughput of 3.125 trains, the passengers now experience a 35 minute travel time instead of 6 minutes.
We can easily observe this drop in throughput in the plot of the full USL equation using 𝛾=1000, 𝛼=0.1, and 𝛽=0.01.
Chart 4: Bounded & Regressive scaling, where once load exceeds N_critical, throughput begins to drop. If load continues increasing, throughput will eventually drop to 0 (over a very long tail).
This kind of situation can result in a catastrophic drop in throughput and complete system failure. Even though all we did was try to increase passenger capacity in the monorail system by adding trains. Despite our good intentions, the system collapsed.
What Does it Have to do with Data Systems?
Data systems aren't all that different from the monorail example. Monorails make for a good mental model for two specific reasons:
Data systems are built around storage and access: data at rest, and data in motion, respectively. IO channels and network sockets operate in a way that is very similar to a monorail, sending fixed-sized packets (in bytes) up and down a channel with a bounded bandwidth. Since channels are ultimately physical, they experience the same bounded & regressive performance characteristic of the monorail example. Message queue and log-based systems exhibit similar patterns as well.
Data systems are built with finite resources that scale much more slowly than changes to the size of the workload. A big spike in queries against a database can have many downstream effects depending on the type and distribution of the queries, and some of those effects can be harmful and even completely catastrophic. The same queuing that occurs when we add too many trains on the track is mirrored when we add too many passengers to the station — people end up waiting longer at the station before they can get on a train, and everything downstream is delayed: their jobs, shopping, making dinner for their children, and so on. Excessive queuing disrupts people’s lives.
A good way to think about data systems in this context is that, even though these days you can provision additional resources and scale your system, it still takes time to copy physical data between servers to rebalance a distributed database, or to read (i.e. copy a subset of) remotely stored data, as is the case with object store databases in the decoupled storage-compute model.
In either case, there is a finite amount of bandwidth as experienced by the user. When either of
the number of concurrent queries
the amount of background maintenance work triggered by the workload
the volume of data needing to be moved (such as when responding with a very large result)
exceed the throughput capacity of the system, what follows is queuing and high pressure as the system struggles to balance the active workload while also managing the thundering herd of new requests coming in and waiting to be served.
And if (or rather when) this queuing capacity reaches its own finite limit (usually bounded by memory or disk space on frontend machines or intermediate workload controllers), then something gives: work needs to be refused, dropped, or, perhaps the worst-case scenario, the system crashes*.
*In a user-centric view, the system crash isn’t any different from refusing and dropping work, since as far as the user is concerned, their needs aren’t being served.
Data systems are particularly susceptible to this pattern of scaling to the point of failure, because they typically handle workloads whose size varies based on external factors. Whether it’s a spike in user requests due to a viral effect, a sudden surge in error logs from a system that doesn't usually emit many errors, or an unintentional thundering herd of requests caused by some third party infrastructure, an uncontrolled increase in load can bring down your system--and the business along with it.
Conclusion
The reality is that every system out there, whether it's a static website, a massive ecommerce platform, a single server database, or a distributed modern cloud database, exists exclusively in the third version of the scaling model, with bounded and regressive scaling.
This means that all systems are at risk of experiencing catastrophic failures from over-scaling. It can lead to full-blown service and revenue impacting outages due to too big an increase in load. These outages are often triggered by load increased because of factors outside of your control.
However, the design of your system, and therefore its scaling mechanics, are within your control, and you should therefore plan and design to be able to determine what your peak manageable load scale is, as well as a means to change your system mechanics in an emergency to allow yourself more time to get the load under control. You basically want the ability to either push yourself back to the left on the chart, or push the inflection point to the right. It won't be cheap, and you may not want to deploy this mitigation for very long, but this is what it means to design for resiliency.
So whenever you engage with infrastructure providers, whether for cloud or on-premise resources, and whether hardware, software, or external services via API access, you should always be asking:
Can the critical limit points of these systems be determined?
Are there ay resources and parameters that will allow you (or your vendor) to change the critical limit characteristics in an emergency?
How, when, and how quickly will these changes be engaged?
What will it cost?
And finally, you should always ask yourself: what limits am I introducing when I'm composing or coupling multiple systems together?
Post-Conclusion: Universal Scalability Law in Practice
Okay, so I'm interested in doing this, but how do I measure these values?
I’m glad you asked! A fair warning, this part involves more math. But I promise it’s worthwhile.
Measuring 𝛾
𝛾 is the throughput when the load multiple is 1, and also the slope of the curve in the early phases of scaling where the system scales more or less linearly.
X(1)= 𝛾∗1=𝛾
Finding the Critical Limit Value
When you know α and β
If you can measure α and β or you know them in advance, you can calculate the critical load value:
Eq. 2: Ncritical
And then plug it into the USL equation to obtain the critical throughput value:
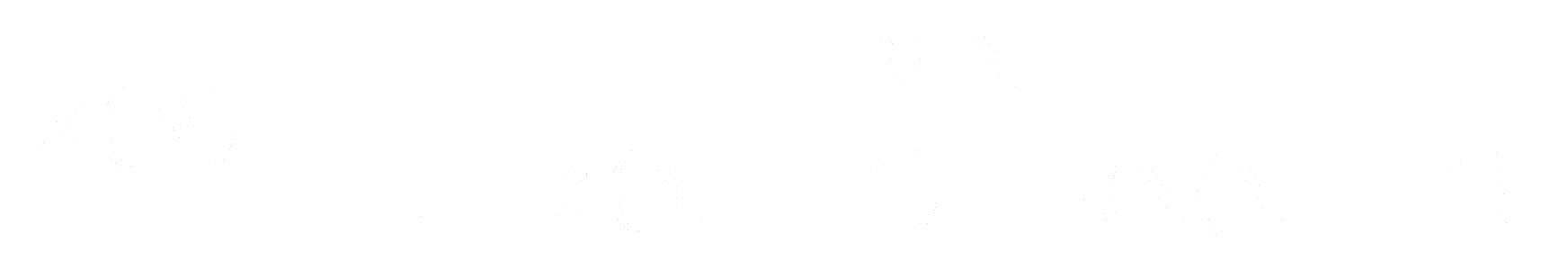
Eq. 1: USL Equation
When you can't measure α or β
This is obviously harder, because we want certainty and, well, we can't have it.
You can, however, measure your throughput vs. load data as your system scales and fit a normally distributed probability density function1,2 to it:
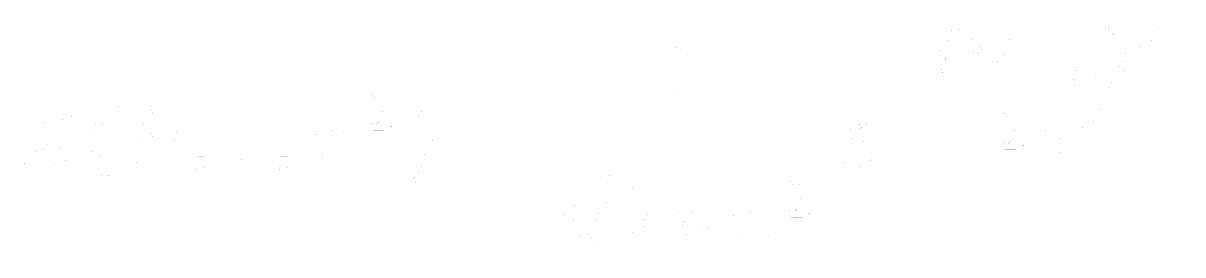
Eq. 6: Probability Density Function (PDF) over a normal distirbution
1: The wikipedia article uses f(x) notation, but here we swap f(x), with X(N) to stay consistent with Gunther's USL notation.
2: This works because the early parts of the USL distribution are roughly normally distributed over log10(N). If you use N’ = log10(N) in the PDF equation, you can then solve for μ.
The median point of the PDF, given by the mode µ, is approximately equal the load at which the critical limit value occurs.
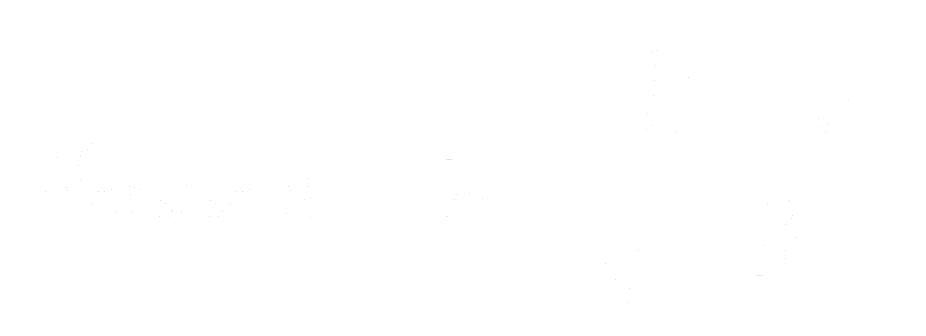
Eq. 7: Ncritical as given by µ
Which then gives us the relationship between α and β
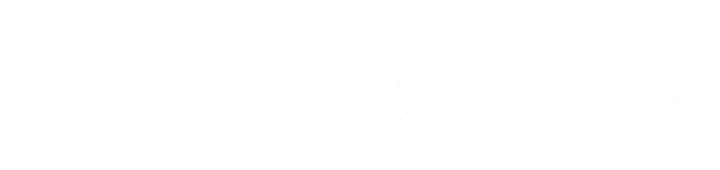
Eq. 8: α and β's relationship in terms of Ncritical
The Issue with the Universal Scalability Law
The problem with Gunther's USL equation is that it's basically impossible to use first principles to construct a system that satisfies a particular set of parameter values for α, β, and γ.
But we obviously want to do this. Constructing systems from first principles is, in fact, the whole point. In order to do this, we will need to connect the 6 physical properties from chapter 1 to the three parameters in Gunther's USL equation.
Stay tuned, as we will cover this in the next chapter of the series.










